ブルーバックスの確率統計で暴くギャンブルのからくり　谷岡一郎　　-絶対儲かる方法のウソ-　読んでみた　期待値、大数の法則、分散のイメージが何となくつかめた気がする

 

スポンサーリンク

確率統計で暴くギャンブルのからくり 谷岡一郎絶対儲かる方法のウソ　ざっくり感想

http://bookclub.kodansha.co.jp/product?item=0000194313

なぜこの本を選んだかと言うと、株式トレードなどのギャンブル&ランダム性のある取引をする際、期待値、大数の法則、分散という三つの法則というか、大きな考え方の理解が必要になってくるためだ。

 

スポンサーリンク

わからないのは、期待値と分散、大数の法則はなんとなくわかる

大数の法則は色々な確率の事象、例えば1/2の確率の事象も少ない試行回数であれば 1/2 の確率に収束することは少ないが、数多くこなしていくと1/2の確率に収束するという考えであり、これはなんとなくイメージが自分でもついた。

大数の法則とは、つまり以下のようなことです。

「ひとつひとつの事象や、短期間での一連の事象においては、どんなに不思議と思われることが起こりえたとしても、充分に大きな回数行われる事象においては、より理論上正確な予想値に収束していく」

「ツキの法則」　谷岡一郎　※本記事で書評してる本とは違う本です、似たようなテーマをあつかってますが

だが期待値と分散という考え方がまったく理解ができなかったため（語感でなんとなくのイメージ程度はつくが）本を読んで概要だけでも理解しようと思いこの本を読んでみることとした。

結論から言うと数式などは理解できなかったが期待値と分散についてなんとなくのイメージはついた。

期待値とは何か

期待値の考え方というのはギャンブルを数学的確率論的に理解する第一歩として最も基本的な概念である。

重要な概念として、期待値と控除率があるということだ。

期待値と控除率は対になった概念で一方が理解できれば他方は自動的に理解されたことになるとのこと。

ざっくり言うと期待値というのは以下の数式により%で表すことができるらしい。

期待値=理論上平均して戻ってくる金額／実際にかける金額×100

もし一回につき1000円かかるゲームがあって、平均して850円戻って来るならこの賭けの期待値は85%ということだ。

85%=850円／1000円×100

つまり言葉で定義するとすれば期待値とは

ある特定の賭け方に対し理論上戻ってくる割合、

である。

ちなみに通常の場合、期待値はパーセントで表示するのが便利であるとのこと。

期待値の例題

あなたは一回100円でダイスをふることができる

もし1か2が出ればあなたの負けであなたは100円を失う

もし3か4が出れば50円戻ってくる。つまりかけ金を考慮すると50円損する

5が出れば100円戻ってきてチャラ

そしてもし６が出ると、500円は350円になって戻ってくるつまり250円のプラス

さてこの影の期待値パーセントはいくらかダイスは正規のものとする

1から6の何れも出る可能性は1/6であり=16.67%であるため、ダイスを6回振れば１から6が一回ずつ平均して出るはず、なので6回振ったものとして考えてみる。

つまりトータルの掛け金額は600円=100円×6回である。

結局かけた一連の金額600円に関して対して理論上平均して550円（-100-100+50+50+100+350）戻ってくることになるつまり50円損をする従って期待値は以下のとおり

このダイスゲームの期待値は

550円／600円×100=91.66%

ということらしい、うん難しい。

数式が掛け算だけなのでまだマシだが、なんとなく難しく感じる。

ちなみに控除率は、 100％から期待値の%を引いた%のことである 。

大数の法則とは何か

大数の法則をわかりやすく表現すると、個々の事象の予測は無理もしくは極めて困難であっても十分に多くの試行がなされた場合、全体的な分布はかなり正確に予測しうるということだそうだ。

あまりよくわからないけど要するに試行回数が大きくなればなるほど理論上の分布過去割合に収束していくということ。

大数の法則は数学上の絶対の真理であって前に述べたようにギャンブルの胴元がわずかな控除率（100％から期待値の%を引いた%が控除率となる）を持つだけで確実に収益が計算できるのは、多くの人が何回もかけることで一定の分布に収束していくということが確実だからである。

胴元にとっては総額でかけられた金額こそが重要なことで、特定個人が少々派手に勝とうが負けようがそんなことはどうでもいいということらしい。

つまり期待値プラスの賭けであれば何度もやれば必ず勝てる、しかし期待値マイナスの通常の胴元のいるようなギャンブルは、やればやるほど負ける必ず負けるということである 。

この大数の法則かを打ち破ることは不可能だが、運良く逃れる可能性を高くする方法が存在するそうだ、それは十分な数だけプレイしないようにするということである。

何度もプレーしてしまうと必ず期待値の数値に収束する。

掛け金額を少なくしたり増やしたりしてゲームをすることや、大穴狙いをするというのも対数の法則から逃れる方法だということだ。

わかりやすくいうと大穴狙いを一発で狙って勝ち逃げするということだ。

これはつまり分散を大きくするということらしい 。

分散とは何か

分散が大きいとは、要はデータのばらつきが大きいということらしい。

この本で具体的に分散がどうだ、ということは書かれていないがそれっぽいことは書かれている。

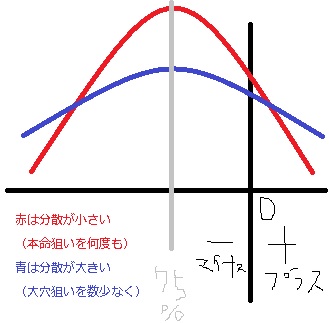
正規分布の幅が違うことを分散が異なるという表現をするそうだ、要はどういうことなのか。

式にすると以下のようなことらしいがイメージがわかない

分散=((データ-平均値)の２乗)の総和÷個数

標準偏差=(分散)の平方根

正規分布の山は 山が高い=高いということが高いということは分散が小さく、低い方は 分散が大きいということだ。

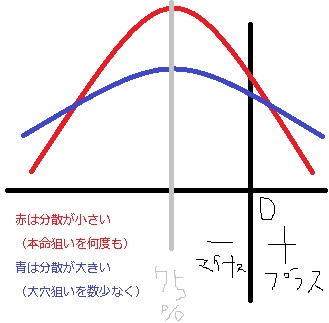
それぞれの事象が起こる確率がばらけてる＝分散が大きい、という意味のようだ。

つまり期待値がある一定のギャンブルをする時（例えば競馬の期待値は この本によると約75%だそうだ）、大数の法則によって競馬をやればやるほど本来の期待値である75%に近づき損をしてしまう。

しかし大穴狙いをした場合は釣鐘型の分布が低くなる、釣鐘形の高さが低くなる大物狙いをした人は 75%付近に収束しづらく、プラスの人が多くなる 、しかしマイナスももっと多くなるということになる。

つまり期待値の低いかけで勝つ方法はないが、その中で勝ち逃げを目指すのであれば分散の大きい方にかけるべきということになる。

分散が小さいということはそのギャンブルの期待値に収束してしまうため例えば競馬であれば本命の馬券を数を買う買うと大数の法則によって期待値を75%に必ず収束してしまう。

しかし大穴狙いを少なくなると分散が大きいためプラスになって勝ち逃げできる可能性も出てくるただし大きくマイナスの人もたくさんいるのでリスクは当然高くなるということだ。 

もっと詳しく知りたい方は以下サイト参照。

https://sci-pursuit.com/math/statistics/variance.html

感想

期待値、大数の法則、分散のイメージが何となくつかめた。

結局期待値が100を超えているのであれば、回数をこなせばこなすほど大数の法則により、期待値に収束するのでそのゲームをやり続ければ良い。そして分散は小さい方が100を超えている期待値に早めに収束しやすいので、収支は早めにプラスになるだろう。

期待値が100以下であれば大数の法則により、回数をこなせば負けるだけだが、大穴狙いなどで試行回数を少なくし、分散をあえて大きく取ることで収支プラスで勝ち逃げられる可能性もある、ただし大きくマイナスになる可能性も当然ある。

あとは実感として実際の取引に落としこめれば良いのだが、例えば株式トレードでいうと期待値の計算てどうやってやるのかわからないし、そんなに実感するほど回数をつめないかもなぁ、と思った（粉）。